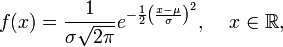DISTRIBUCIÓN NORMAL: noviembre 2011

DISTRIBUCIÓN NORMAL

La distribución normal es una de las distribuciones más usadas e importantes. Esta se ha convertido en una herramienta que se utiliza en la mayoría de las ramas de la ciencia por no decir todas , también se aplica en gran parte de la industria y el comercio. Muchos eventos cotidianos tiene un gran parecido a la distribución normal ya que esta se utiliza para describir el conjunto de datos que muestran la frecuencia con que ocurren ciertas cosas en la naturaleza y en la industria.

Por ejemplo:

Las características básicas de una persona: altura, peso, número de pie

Las características de la mayoría de los productos : duración de los bombillos, duración de los electrodomésticos.

Calificaciones obtenidas en cursos, asignaturas y exámenes.

A este tipo de distribución también se le conoce como campana de Gauss por la forma de sus gráficas

Hay varias maneras de definir una distribución, La forma más común es mediante su función de densidad que no es mas que la función que caracteriza el comportamiento probable de las cosas.

Se dice que una variable aleatoria continua X sigue una distribución normal de parámetros μ y σ y se denota X~N(μ, σ) si su función de densidad está dada por:

$f(x)=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2}, \, \quad x\in\mathbb{R},$

donde μ (miu) es la media y σ (sigma) es la desviación típica (σ² es la varianza).

En la distribución normal μ y σ toman otros valores μ = 0 y σ = 1.

Así la función de densidad tiene la siguiente expresión, según la distribución normal:

$f(x)=f_{0,1}(x)=\frac{e^\frac{-x^2}{2}}{\sqrt{2\pi\,}}, \,\quad x\in\mathbb{R}.$

ejemplo:

Si X es una variable aleatoria de una distribución N(µ, σ), hallar:
p(µ−3σ ≤ X ≤ µ+3σ

Es decir, que aproximadamente el 99.74% de los valores de X están a menos de tres desviaciones típicas de la media.

Felix S. Perez
C.I.:21.245.309

3T1IS

PROPIEDADES DE LA DISTRIBUCIÓN NORMAL

La distribución normal posee ciertas propiedades a las cuales cabe resaltar entre ellas tenemos las siguientes:

· la curva tiene un solo pico, por consiguiente es unimodal. presenta una forma de campana.

La media de una población distribuida normalmente se encuentra en el centro de su curva normal.
La causa de la simetría de la distribución normal de probabilidad, la mediana y la moda de la distribución también se hallan en el centro, por tanto en una curva normal, la media, la mediana y la moda poseen el mismo valor.
Las dos colas (extremos) de una distribución normal de probabilidad se extienden de manera indefinida y nunca tocan el eje horizontal.

Áreas bajo la curva normal.

El área total bajo la curva normal será de 1.00 por lo cual podemos considerar que las áreas bajo la curva son probabilidades.

La forma de la campana de gauss depende de los parámetros μ y σ la media indica la posición de la campana, de modo que para diferentes valores de μ la gráfica es desplazada a lo largo del eje horizontal. Por otra parte, la desviación estándar determina el grado de apuntamiento de la curva. Cuanto mayor sea el valor de σ , más se dispersarán los datos en torno a la media y la curva será más plana. Un valor pequeño de este parámetro indica, por tanto, una gran probabilidad de obtener datos cercanos al valor medio de la distribución.

Como se deduce de este último apartado, no existe una única distribución normal, sino una familia de distribuciones con una forma común, diferenciadas por los valores de su media y su varianza. De entre todas ellas, la más utilizada es la distribución normal estándar, que corresponde a una distribución de media 0 y varianza 1. Así, la expresión que define su densidad se puede obtener resultando:

El valor de z.

z= número de desviaciones estándar de x respecto a la media de esta distribución.

z= x-m / s

x=valor de la variable aleatoria que nos interesa.
m= media de la distribución de esta variable aleatoria.
s = desviación estándar de esta distribución.

Las variables aleatorias distribuidas en forma normal asumen muchas unidades diferentes de medición, por lo que hablaremos de forma estándar y les daremos el símbolo de z.

ejemplo:

Si deseamos la probabilidad de que una persona, elegida al azar, tenga un peso mayor o igual a 150 libras.

Paso 1 Interpretar gráficamente el área de interés.

Gráficamente si decimos que a=150 libras, el área de la curva que nos interesa es :

Jose G. Escalona O.

C.I: 22.264.793

3T1IS

ESPERANZA Y VARIANZA

Esperanza

Los nombres de esperanza matemática y valor esperado tienen su origen en los juegos de azar y hacen referencia a la ganancia promedio esperada por un jugador cuando hace un gran número de apuestas.

Si la esperanza matemática es cero, E(x) = 0, el juego es equitativo, es decir, no existe ventaja ni para el jugador ni para la banca.

Ejemplos

Si una persona compra una papeleta en una rifa, en la que puede ganar de 5.000 € ó un segundo premio de 2000 € con probabilidades de: 0.001 y 0.003. ¿Cuál sería el precio justo a pagar por la papeleta?

E(x) = 5000 · 0.001 + 2000 · 0.003 = 11 €

Un jugador lanza dos monedas. Gana 1 ó 2 € si aparecen una o dos caras. Por otra parte pierde 5 € si no aparece cara. Determinar la esperanza matemática del juego y si éste es favorable.

E = {(c,c);(c,x);(x,c);(x,x)}

p(+1) = 2/4

p(+2) = 1/4

p(−5) = 1/4

E(x)= 1 · 2/4 + 2 · 1/4 - 5 · 1/4 = −1/4.

Es desfavorable

Desviación estándar

La desviación estándar (σ) mide cuánto se separan los datos.

La fórmula es fácil: es la raíz cuadrada de la varianza. Así que, "¿qué es la varianza?"

Varianza

La varianza (que es el cuadrado de la desviación estándar: σ²) se define así:

Es la media de las diferencias con la media elevadas al cuadrado.

En otras palabras, sigue estos pasos:

Calcula la media (el promedio de los números)
Ahora, por cada número resta la media y eleva el resultado al cuadrado (la diferencia elevada al cuadrado).
Ahora calcula la media de esas diferencias al cuadrado.

Ejemplo

Tú y tus amigos han medido las alturas de sus perros (en milímetros):

Las alturas (de los hombros) son: 600mm, 470mm, 170mm, 430mm y 300mm.Calcula la media, la varianza y la desviación estándar.

Respuesta:

Media =	600 + 470 + 170 + 430 + 300 =	1970 = 394

	5	5

así que la altura media es 394 mm. Vamos a dibujar esto en el gráfico:

Para calcular la varianza, toma cada diferencia, elévala al cuadrado, y haz la media:

Varianza: σ² =	206² + 76² + (-224)² + 36² + (-94)²	=	108,520	= 21,704

	5		5

Así que la varianza es 21,704.

Y la desviación estándar es la raíz de la varianza, así que:

Desviación estándar: σ = √21,704 = 147

Propiedades de la varianza

Si X es una variable aleatoria con función de probabilidad o densidad f(x), la varianza de una función de la variable X , m(x) , se calcula según la expresión:

Casos concretos:

1. Cuando a todos los valores de una variable se les suma una constante, la varianza de la variable conserva el mismo valor (ver imagen en las propiedades de la media)

2. Cuando a todos los valores de una variable se les multiplica por una constante, la varianza de la variable queda multiplicada por el valor de la constante elevado al cuadrado (ver imagen en las propiedades de la media)

3. Si X e Y son dos variables aleatorias con función de densidad o probabilidad conjunta f(x,y), la varianza de la función m(x,y) = a X ± b Y, donde a y b son constantes reales se calcula como:

En el caso de que a = b = 1

Si además ocurre que X e Y sean independientes σ_xy = 0 , luego

Jocelin C. Quero.

C.I.: 21.274.430

3T1IS

EJEMPLOS

Ejemplo 1: El gerente de personal de una gran compañía requiere que los solicitantes a un puesto efectúen cierta prueba y alcancen una calificación de 500. Si las calificaciones de la prueba se distribuyen normalmente con media 485 y desviación estándar 30 ¿Qué porcentaje de los solicitantes pasará la prueba?

Calculando el valor de Z obtenemos:

Buscamos el valor correspondiente Z en la tabla de distribución normal. Z_0.5 = .69146 = 69.146%. siendo esta la probabilidad de que la calificación sea menor a 500 P (X<500). Dado que el porcentaje pedido es la solución es 1-.69146 =.3085, 30.85% de los participantes pasarán la prueba.

Ejemplo 2:

Encuentre las probabilidades siguientes usando la tabla Z.

a) P(-1.23 < Z > 0)

Solución: Buscamos el valor Z_1..23 en las tablas siendo este = .89065. restando .89065-.05 = .3905, este valor es la probabilidad de 0 a 1.23 que es exactamente la misma de –1.23 a 0 por simetría. Por lo tanto la probabilidad es .3905

Ejemplo 3: Haciendo uso de la tabla que proporciona áreas a la izquierda de cada valor z de la distribución normal

tipificada, calcular las probabilidades (áreas)

Siguientes:

a) Pr (z<1'35)

b) Pr (z<-0'338)

c) Pr (z>2'1)

d) Pr (z>-1)

e) Pr (-1'39<z≤-0'44)

f) Pr (-1'52≤z≤0'897)

Observe que, en el cálculo de áreas (probabilidades) en variables continuas, Pr(x≤a) equivale a Pr(x<a).

Tendremos que referir los cálculos a probabilidades del tipo Pr(z < a) , estando expresado el valor a con dos cifras

decimales :

Jhonathan R. Rivero M.
C.I.:20.943.222
3T1IS

domingo, 13 de noviembre de 2011